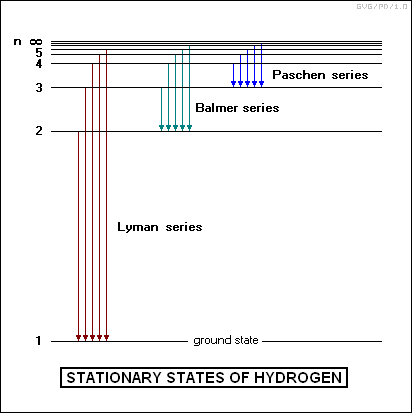
Spectral LinesAtoms, as well as molecules, have discretized energy levels. When an electron is least energetic it occupies the ground state (n=1). The next level an electron can reside in is the first excited state (n=2). The difference between these energy levels and any other level is discretized. For example, hydrogen's energy levels are defined by: (3)\begin{align} \definecolor{blue}{rgb}{.525,.631,.922}\pagecolor{blue} E_n=-13.6 [eV]\frac{1}{n^2}=\frac{-\alpha^2 m_e c^2}{2}\frac{1}{n^2} \end{align}
The transition between two levels is the difference in these energies: (4)\begin{align} \definecolor{blue}{rgb}{.525,.631,.922}\pagecolor{blue} \Delta E_{n_1\rightarrow n_2}=\frac{\alpha^2 m_e c^2}{2}(\frac{1}{n_2^2}-\frac{1}{n_1^2}) \end{align}
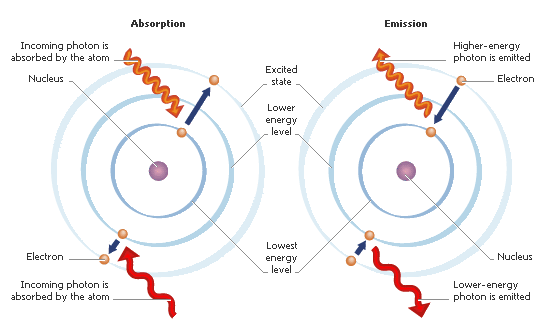
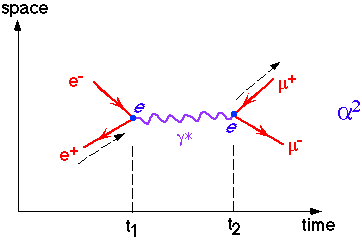
If an electron loses or gains this quantized energy1 it can transition to the associated energy level. A quanta of light, the photon, transmits the energy of these transitions. (5)\begin{align} \definecolor{blue}{rgb}{.525,.631,.922}\pagecolor{blue} E_{photon}=h \nu = \frac{h c}{\lambda} \end{align}
|
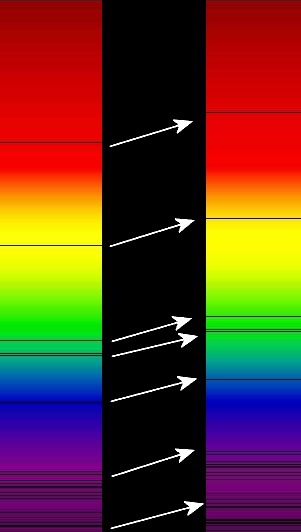
Absorption LinesA coherent source of light passing through a gas will have photons of particular wavelengths missing. This occurs since photons with a particular energy and thus a particular wavelength are absorbed and later re-emitted. The direction of the re-emission is determined by momentum conservation of the initial and final states2. The wavelength of the absorbed photon will appear to be missing because the emission is not necessarily in the same direction as it was absorbed. At this wavelength the coherence of the light source is destroyed leaving a hole of varying depth in the flux of light detected. |
RedshiftThe amount by which wavelength changes is determined by redshift, (6)\begin{align} \definecolor{blue}{rgb}{.525,.631,.922}\pagecolor{blue} z=\frac{\lambda_{obs} - \lambda_{emit}}{\lambda_{emit}}= \frac{\lambda_{obs}}{\lambda_{emit}}-1 \end{align}
This dimensionless quantity is measured relative to an observer. For PHL957, z is approximately +2.3 implying a redshift instead of a blueshift. The fact that z is positive means the object is moving away, stretching the wavelength, and "shifting" its visible light towards the red end of the spectrum. This redshift is the basis for the theory of an expanding universe since all observed light sources from far outside of our galaxy are redshifted3. |
Scale FactorThe metric is separable into a time and space component in the previous equation but the new scale factor is time dependent. Since the redshift is dependent only on the time of emission and observation: (9)\begin{align} \definecolor{grey}{rgb}{.380,.380,.380}\pagecolor{grey} z= \frac{a_{obs}}{a_{emit}}-1=\frac{#1}{a_{emit}}-1 \end{align}
(10)
\begin{align} \definecolor{grey}{rgb}{.380,.380,.380}\pagecolor{grey} a_{emit}=\frac{#1}{z+1} \end{align}
where the observed scale factor is taken to be 1 since redshift only has significance relative to the observer. Assuming a big bang model one can infer that the scale factor and thus the redshift can tell us how old the light source is4. |